中1数学 | 7th Grade Math
整数の性質
Properties of Integers
TARGET
整数のきまりを覚えよう
自然数 (しぜんすう)
自然数とは、「1」、「2」、「3」など、1以上の整数のことです。「0」は自然数ではありません。
素数 (そすう)
素数とは、「2」、「3」、「5」、「7」など、1とその数自身の積でしか表わせない自然数のことです。
1は素数ではありません。「1×別の数字」で表せないからです。
2は素数です。「1×2」以外の積で表せないからです。
3は素数です。「1×3」以外の積で表せないからです。
4は素数ではありません。「1×4」以外に「2×2」でも表せるからです。
5は素数です。「1×5」以外の積で表せないからです。
考え方1から20までの素数をすべて求めてみましょう。
よって、2,3,5,7,11,13,17,19が答えです。
素因数 (そいんすう)
自然数をいくつかの素数の積で表すとき、それらの素数をもとの自然数の素因数と言います。例えば、30を「2×3×5」と表すとき、「2」、「3」、「5」が30の素因数です。
素因数分解 (そいんすうぶんかい)
素因巣分解とは、自然数を素因数だけの積の形で表すことです。
例えば、60を素因数分解すると下記のように表わすことができます:

累乗 (るいじょう)
「2 × 2」や「2 × 2 × 2」のように、同じ数をいくつか掛け合わせたものを、その数の累乗といいます。例えば、「2 × 2 × 2」を「23」と表します。「23」は「2の三乗(さんじょう)」と読み、右上に小さく書いた数字は掛けた個数を表し、これを累乗の指数と言います。
練習問題
Q 0160を素因数分解しなさい。
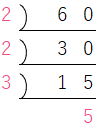
60 = 2 × 2 × 3 × 5 = 22 × 3 × 5
Q 0272を素因数分解しなさい。
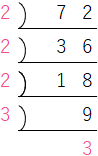
72 = 2 × 2 × 2 × 3 × 3 = 23 × 32
Q 03150を素因数分解しなさい。
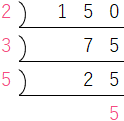
150 = 2 × 3 × 5 × 5 = 2 × 3 × 52
Q 04素因数分解を利用して、180の約数をすべて書きなさい。
まず、180を素因数分解します。
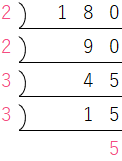
180 = 2 × 2 × 3 × 3 × 5
ここで、すべての自然数の約数である1と、素因数は約数となります。
すべての自然数の約数:1
素因数:2, 3, 5
次に、素因数と素因数の積も約数となるので、その組み合わせを考えます。
素因数2つの積の組み合わせ:
2 × 2 = 4, 2 × 3 = 6, 3 × 3 = 9, 2 × 5 = 10, 3 × 5 = 15
素因数3つの積の組み合わせ:
2 × 2 × 3 = 12, 2 × 3 × 3 = 18, 2 × 2 × 5 = 20, 2 × 3 × 5 = 30, 3 × 3 × 5 = 45
素因数4つの積の組み合わせ:
2 × 2 × 3 × 3 = 36, 2 × 2 × 3 × 5 = 60, 2 × 3 × 3 × 5 = 90
素因数5つの積の組み合わせ:
2 × 2 × 3 × 3 × 5 = 180
したがって、これら18個が180の約数となります。
1, 2, 3, 4, 5, 6, 9, 10, 12, 15, 18, 20, 30, 36, 45, 60, 90, 180
Q 05素因数分解を利用して、60と90の最大公約数と最小公倍数を求めなさい。
最大公約数とは、共通する約数(割り切れる数)の中で一番大きい約数のこと。
最大公約数を求めるには、60と90を一緒に素因数分解し、2つの自然数に共通する素因数を見つけ、それを掛け合わせます。
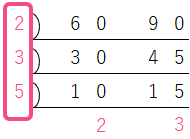
2 × 3 × 5 = 30
最大公約数は30
最小公倍数とは、共通する倍数の中で一番小さい倍数のこと。
最小公倍数を求めるには、60と90を一緒に素因数分解し、2つの自然数共通する素因数と、残った商をすべて掛け合わせます。
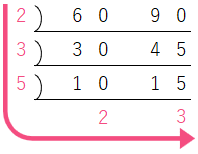
2 × 2 ×3 × 3 × 5 = 180
最小公倍数は180
Q 0672にできるだけ小さい自然数nをかけて、ある自然数の2乗になるようにしたい。nはいくつにすればよいか求めなさい。
まず、72を素因数分解します。
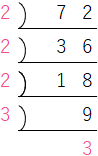
72 = 2 × 2 × 2 × 3 × 3
ある自然数の2乗になるということは、素因数分解すると同じ数でペアを作れるということです。下の式を見ると、ペアになっていない「2」があります。
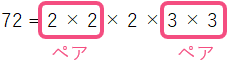
このペアになっていない「2」に「2」をかけるとペアができます。
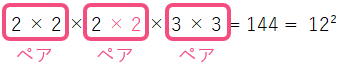
したがって、答えは n = 2 となります。
因数分解では、10までの素数「2, 3, 5, 7」を覚えておき、これらの数で割れるかどうかを考えてみよう。
TERMS
数学分野の英語表現を学ぼう
Natural Number / nǽtʃərəl / nʌ́mbər / ナチュラル ナンバー |
自然数 Natural numbers are the numbers we use when counting things. 自然数とは、数を数えるときに使う数のことです。 |
|---|---|
Prime Number / práim / nʌ́mbər / プライム ナンバー |
素数 A prime number is a natural number greater than 1 that can only be divided by 1 and itself. 素数は1とその数以外で割り切れない、1より大きい自然数です。 |
Prime Factor / práim / fǽktər / プライム ファクター |
素因数 A prime factor is a prime number that divides a number, without leaving a remainder. 素因数とは、余りなくその数を割り切る素数のことです。 |
Prime Factorization / práim / fæktəraɪˈzeɪʃən / プライム ファクタライゼイション |
素因数分解 Prime factorization is the process of expressing a natural number as a product of only prime factors. 素因巣分解とは、自然数を素因数だけの積の形で表すことです。 |
Power / páuər / パワー |
累乗 When you multiply the same number several times, like '2 × 2' or '2 × 2 × 2', it’s called a power of that number. 「2 × 2 」や「2 × 2 × 2」のように、同じ数をいくつか掛け合わせたものを、その数の累乗といいます。 |
Exponent / ekspóunənt / エクスポーネント |
指数 The exponent is the number that shows how many times the base is multiplied by itself in exponentiation. 指数とは、累乗において基数を何回掛けるかを示す数です。 |
累乗の英語表現
【二乗】
52は、five squared、または、the square of fiveと言います。
【三乗】
53は、five cubed、または、the cube of fiveと言います。
【その他の累乗】
54は、five raised to the power of four、または、five to the fourと言います。

